Reading a Tree Diagram Flipping a Coin

Tree Diagrams — An easy way to Sympathise Probability

Probability is the chance that a certain effect will happen or the likelihood of some upshot will happen. Knowing probability and its applications is of import because statistical inference uses probability distributions of the data. Having a adept knowledge of probability is a must for an aspiring data scientist and data analyst. Reading this writing enables you to reply questions similar:

1. The probability of having a head when flipping a coin once? — 50% of course.
2. What is the probability of having exactly two heads and iii tails when flipping a coin three times?
3. What is the probability of throwing tails first, and then heads, so tails, then heads, and so tails when flipping a money 5 times?
4. What is the probability that both numbers are less than five or odds if two dice are thrown together?
5. Or just what are the chances of no delays on a circular trip if the chance of a flight being delayed is 0.2 (20%)…etc.

Answer 1 & 2: A money has 2 faces: 1 caput and a tail. That is counted as 2 as probable outcomes (caput, tail) for one independent issue — flipping a coin one time. So, the probability of getting a head when flipping a coin one time is 50%. With flipping the money 3 times, we take three contained events here. The total outcomes must exist 2³ = 8 outcomes. The outcomes of a sample infinite are called every bit likely if all of them have the same run a risk of occurring. The probability of getting a head is equal to the probability of getting a tail in the first toss and is ½. The second time y'all toss the coin, the probability of getting a head is the same as the first time you toss the coin and is ½. Probability of getting a head is besides ½ the 3rd time you toss. Let's expect at the tree diagram beneath that shows all the possible outcomes of flipping a coin iii times.

How do we summate the overall probabilities?

• Commencement, we multiply probabilities each time nosotros toss beyond the rows
• 2d, we add together probabilities across the columns

Now allow's see:

• All the probability add up to 1
• The probability of getting 3 Heads "HHH" is ½ x ½ x ½ = ⅛
• The probability of getting 3 Tails "TTT" is ½ x ½ x ½ = ⅛
• The probability of getting at least 1 Head "HHH, HHT,HTH,HTT, THH,THT,TTH" from three tosses is 1/8 + ane/8 + 1/8 + 1/eight + ane/8 + 1/viii + ⅛ = ⅞ and this is also equal the probability of getting at least i tail from three tosses which is ⅞.
• The probability of getting exactly 2 heads and 3 tails when a coin is flipped iii times is = probability of getting exactly 2 Heads "HHT,HTH,THH" + probability of getting 3 tails "TTT" = (1/eight + i/8 + 1/8) + ⅛ = i/two

A three: Then, what is the probability of throwing tail first, then head, and so tail, and so caput, then tail when flipping a coin 5 times? Nosotros don't take to work difficult to effigy this out. From the tree diagrams, this is what nosotros go: P(THTHT) = ½ x ½ x ½ x ½ 10 ½ = ane/32

A4 -a: There are six possible equally likely outcomes on a die: {one,2,3,four,5,6}.

There are 4 numbers less than five: {i,two,3,iv} and two numbers are greater than or equal to 5: {v,6}.

The probability of getting a number less than five is 4/six = ⅔, and the probability of getting a number greater or equal five is two/6 = ⅓.

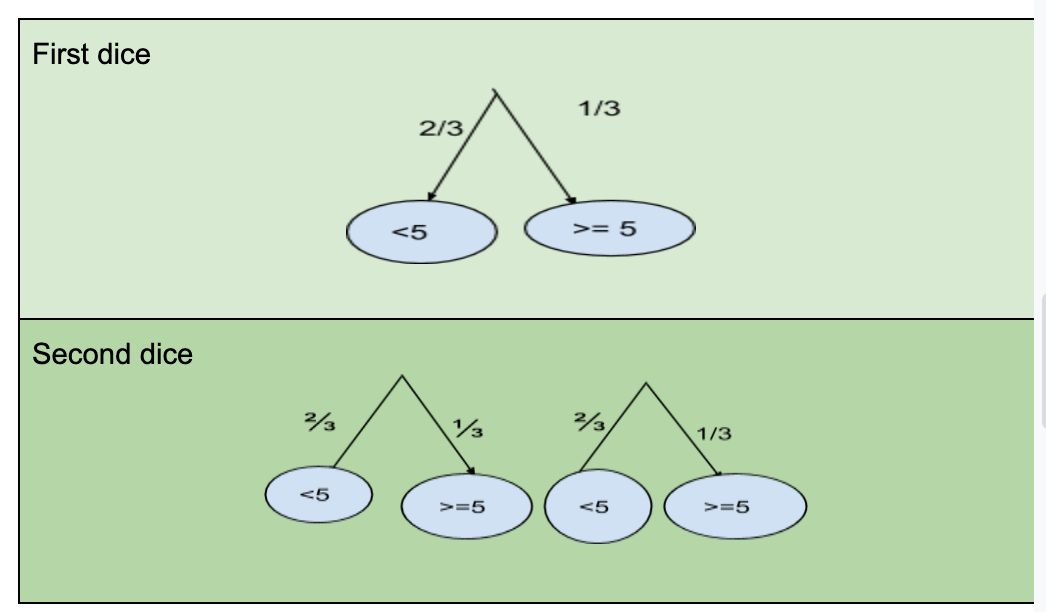
From the tree diagrams, you can come across that the probability that both numbers are less than v is: ⅔ x ⅔ = iv/nine. The probability of getting 1 number less than five and the other greater than or equal v is: 2/three x 1/3 + 2/3 10 one/three = 4/9, and the probability of getting two numbers greater or equal five is one/3 x 1/iii = i/9.

A4-b: Possible outcomes = {one,2,3,four,v,half-dozen} when tossing a dice in the air

Odd numbers ={1,3,five}, even numbers = {2,4,six}

The probability of getting an odd number or even number is 3/6 = ½ . The probability of getting both numbers are odd numbers is ½ x ½ = ¼. Let's double check on the tree diagrams.

A5: The respond to question five is very much familiar to the way nosotros answer to question 4. There are two contained possible outcomes: delay and no-delay. If the probability of being delayed is 0.two, the probability of not beingness delayed is ane–0.2 = 0.8. Let'southward swoop in.

The probability of having no delays on round trips is 0.8 x 0.8 = 0.64 ~ 64%.

The probability of render flight delayed is : 0.8 x 0.two = 0.16

The take a chance of outset flight delayed is: 0.2 x 0.eight = 0.sixteen

And the probability of both flights delayed is: 0.2 x 0.2 = 0.04

To sum upwardly when in dubiousness, you should draw a tree diagram, multiply along the rows and add the columns. Be sure to retrieve that all probabilities add to one.

Happy Learning!

sototoloses.blogspot.com

Source: https://medium.com/@thoashook/tree-diagrams-an-easy-way-to-understand-probability-43db5b231a9b

Share this post